How To Find Helix Angle Of Helical Gear

Introduction

Helical gears are similar to spur gears except that the gears teeth are at an angle with the axis of the gears. A helical gear is termed right handed or left handed as adamant by the direction the teeth slope away from the viewer looking at the tiptop gear surface forth the axis of the gear. ( Alternatively if a gear rests on its face the mitt is in the direction of the gradient of the teeth) . Meshing helical gears must be of opposite manus. Meshed helical gears can be at an angle to each other (upward to 90^o ). The helical gear provides a smoother mesh and can be operated at greater speeds than a straight spur gear. In operatation helical gears generate axial shaft forces in improver to the radial shaft force generated by normal spur gears.

In operation the initial tooth contact of a helical gear is a bespeak which develops into a full line contact as the gear rotates. This is a smoother cycle than a spur which has an initial line contact. Spur gears are generally non run at peripheral speed of more than 10m/s. Helical gears tin be run at speed exceeding 50m/s when accurately machined and balanced.

Standards ... The same standards employ to helical gears as for spur gears

AGMA 2001-C95 or AGMA-2101-C95 Key Rating factors and Calculation Methods for involute Spur Gear and Helical Gear Teeth
BS 436-iv:1996, ISO 1328-1:1995..Spur and helical gears. Definitions and allowable values of deviations relevant to corresponding flanks of gear teeth
BS 436-5:1997, ISO 1328-two:1997..Spur and helical gears. Definitions and commanded values of deviations relevant to radial composite deviations and runout data
BS ISO 6336-1:1996 ..Calculation of load capacity of spur and helical gears. Basic principles, introduction and general influence factors
BS ISO 6336-2:1996..Calculation of load capacity of spur and helical gears. Adding of surface durability (pitting)
BS ISO 6336-3:1996..Calculation of load capacity of spur and helical gears. Calculation of molar bending strength
BS ISO 6336-5:2003..Calculation of load capacity of spur and helical gears. Strength and quality of materials

Helical gear parameters

A helical gear train with parallel axes is very like to a spur gear with the aforementioned tooth contour and proportions. The primary difference is that the teeth are machined at an bending to the gear axis.

Helix Angle ..

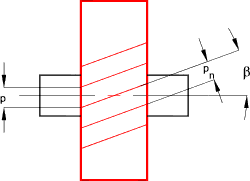
The helix angle of helical gears β is generally selected from the range six,8,10,12,xv,20 degrees. The larger the angle the smoother the move and the higher speed possible yet the thrust loadings on the supporting bearings also increases. In case of a double or herringbone gear β values 25,30,35,40 degrees tin can besides be used. These large angles tin can be used because the side thrusts on the two sets of teeth cancel each other allowing larger angles with no punishment

Pitch /module ..

For helical gears the circular pitch is measured in two ways
The traverse round pitch (p) is the same as for spur gears and is measured along the pitch circle
The normal round pitch p _n is measured normal to the helix of the gear.
The diametric pitch is the same as for spur gears ... P = z _g /d_g = z _p /d _p ....d= pitch circumvolve dia (inches).
The module is the same as for spur gears ... 1000 = d_g/z _m = d _p/z _p.... d = pitch circumvolve dia (mm).

Helical Gear geometrical proportions

p = Circular pitch = d _g. p / z _g = d _p. p / z _p
p _n = Normal circular pitch = p .cosβ
P _n =Normal diametrical pitch = P /cosβ
p _ten = Axial pitch = p _c /tanβ
chiliad _n =Normal module = thou / cosβ
α _n = Normal pressure angle = tan ^-1 ( tanα.cos β )
β =Helix angle
d _g = Pitch diameter gear = z _thousand. m
d _p = Pitch diameter pinion = z _p. m
a =Heart distance = ( z _p + z _chiliad )* m _n /2 cos β
a _a = Addendum = m
a _f =Dedendum = i.25*m
b = Face width of narrowest gear

Herringbone / double crossed helical gears

Crossed Helical Gears

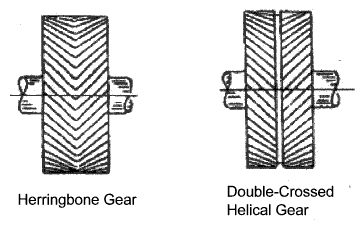
When ii helical gears are used to transmit power between non parallel, non-intersecting shafts, they are generally called crossed helical gears. These are simply normal helical gears with non-parallel shafts. For crossed helical gears to operate successfully they must have the same pressure angle and the same normal pitch. They need non take the same helix angle and they do non need to exist contrary manus. The contact is not a expert line contact as for parallel helical gears and is often little more than than a bespeak contact. Running in crossed helical gears tend to marginally meliorate the area of contact.

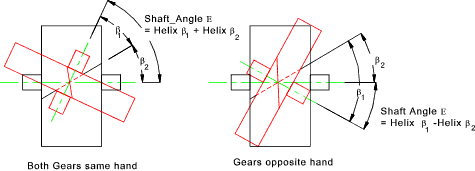
The relationship between the shaft angles

E and the helix angles β ₁ & β_ii is equally follows

Due east = (Same Helix Angle) β _ane + β ₂ ......(Reverse Helix Bending) β _ane - β ₂

For gears with a 90^o crossed centrality it is obvious that the gears must be the aforementioned hand.

The centres distance (a) between crossed helical gears is calculated as follows

a = m * [(z _ane / cos β _one) + ( z _i / cos β ₁ )] / 2

The sliding velocity 5_southof crossed helical gears is given by

V_south = (V₁ / cos β ₁ ) = (V _ii / cos β ₂ )

Strength and Durability calculations for Helical Gear Teeth

Designing helical gears is commonly washed in accordance with standards the two most popular serial are listed under standards above: The notes below chronicle to approximate methods for estimating gear strengths. The methods are really only useful for commencement approximations and/or selection of stock gears (ref links below). � Detailed design of spur and helical gears should best be completed using :

a) Standards.
b) Books are available providing the necessary guidance.
c) Software is also available making the process very easy. A very reasonably priced and easy to utilize package is included in the links beneath (Mitcalc.com)

The determination of the capacity of gears to transfer the required torque for the desired operating life is completed past determining the strength of the gear teeth in angle and also the durability i.eastward of the teeth ( resistance to wearing/bearing/scuffing loads ) .. The equations beneath are based on methods used by Buckingham..

Bending

The Lewis formula for spur gears can be applied to helical gears with minor adjustments to provide an initial bourgeois gauge of gear strength in angle. This equation should only be used for first estimates.

σ = F_b / ( b_a. m. Y )

F_b = Normal force on tooth = Tangential Force F_t / cos β
σ = Tooth Bending stress (MPa)
b_a = Face width (mm)
Y = Lewis Form Factor
m = Module (mm)

When a gear bike is rotating the gear teeth come into contact with some caste of impact. To allow for this a velocity cistron is introduced into the equation. This is given by the Barth equation for milled profile gears.

K _v = (6,i + 5 ) / 6,one

5 = the pitch line velocity = PCD.w/2

The Lewis formula is thus modified every bit follows

σ = One thousand _v.F_b / b_a. m. Y

The Lewis class gene Y must be determined for the virtual number of teeth z' = z /cos³β The bending stress resulting should exist less than the allowable bending stress S_b for the gear material under consideration. Some sample values are provide on this page ef Gear Strength Values

Surface Strength

The allowable gear force from surface durability considerations is determined approximately using the unproblematic equation as follows

F_westward = Yard ₅ d _p b _a Q G / cos²β

Q = 2. d_g /( d_p + d_p ) = two.z_g /( z_p +z_p )

F_w = The commanded gear load. (MPa)

K = Gear Wear Load Cistron (MPa) obtained by look upwards ref Gear Strength Values

Lewis Class factor for Teeth profile α = 20^o, addendum = k, dedendum = ane.25m
Number of teeth	Y	Number of teeth	Y	Number of teeth	Y	Number of teeth	Y	Number of teeth	Y
12	0.245	17	0.303	22	0.331	34	0.371	75	0.435
xiii	0.261	xviii	0.309	24	0.337	38	0.384	100	0.447
xiv	0.277	19	0.314	26	0.346	45	0.401	150	0.460
15	0.290	xx	0.322	28	0.353	fifty	0.409	300	0.472
sixteen	0.296	21	0.328	30	0.359	60	0.422	Rack	0.485