How To Find Distance Of Two Points

Haversine formula to discover altitude betwixt two points on a sphere

The Haversine formula calculates the shortest distance betwixt two points on a sphere using their latitudes and longitudes measured along the surface. It is important for use in navigation. The haversine tin can be expressed in trigonometric part as:

The haversine of the central angle (which is d/r) is calculated by the following formula:

where r is the radius of the earth(6371 km), d is the distance between two points,is the breadth of the two points, andis the longitude of the two points respectively.
Solving d past applying the inverse haversine or by using the inverse sine office, we get:

or

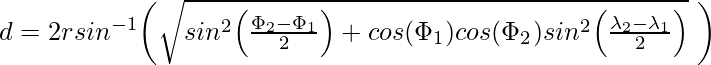
The altitude between Big Ben in London (51.5007° N, 0.1246° Westward) and The Statue of Liberty in
New York (40.6892° N, 74.0445° W) is 5574.8 km. This is not the exact measurement considering the
formula assumes that the Earth is a perfect sphere when in fact it is an oblate spheroid.
Beneath is the implementation of the to a higher place formulae:

C++

#include <iostream>

#include <cmath>

using namespace std;

static double haversine( double lat1, double lon1,

double lat2, double lon2)

{

double dLat = (lat2 - lat1) *

M_PI / 180.0;

double dLon = (lon2 - lon1) *

M_PI / 180.0;

lat1 = (lat1) * M_PI / 180.0;

lat2 = (lat2) * M_PI / 180.0;

double a = pow ( sin (dLat / 2), 2) +

prisoner of war ( sin (dLon / 2), 2) *

cos (lat1) * cos (lat2);

double rad = 6371;

double c = 2 * asin ( sqrt (a));

return rad * c;

}

int primary()

{

double lat1 = 51.5007;

double lon1 = 0.1246;

double lat2 = 40.6892;

double lon2 = 74.0445;

cout << haversine(lat1, lon1,

lat2, lon2) << " G.1000." ;

return 0;

}

Coffee

public class Haversine {

static double haversine( double lat1, double lon1,

double lat2, double lon2)

{

double dLat = Math.toRadians(lat2 - lat1);

double dLon = Math.toRadians(lon2 - lon1);

lat1 = Math.toRadians(lat1);

lat2 = Math.toRadians(lat2);

double a = Math.pw(Math.sin(dLat / two ), ii ) +

Math.pow(Math.sin(dLon / 2 ), 2 ) *

Math.cos(lat1) *

Math.cos(lat2);

double rad = 6371 ;

double c = 2 * Math.asin(Math.sqrt(a));

render rad * c;

}

public static void master(String[] args)

{

double lat1 = 51.5007 ;

double lon1 = 0.1246 ;

double lat2 = 40.6892 ;

double lon2 = 74.0445 ;

System.out.println(haversine(lat1, lon1, lat2, lon2) + " Grand.M." );

}

}

Python three

import math

def haversine(lat1, lon1, lat2, lon2):

dLat = (lat2 - lat1) * math.pi / 180.0

dLon = (lon2 - lon1) * math.pi / 180.0

lat1 = (lat1) * math.pi / 180.0

lat2 = (lat2) * math.pi / 180.0

a = ( pw (math.sin(dLat / 2 ), 2 ) +

prisoner of war (math.sin(dLon / two ), 2 ) *

math.cos(lat1) * math.cos(lat2));

rad = 6371

c = 2 * math.asin(math.sqrt(a))

render rad * c

if __name__ = = "__main__" :

lat1 = 51.5007

lon1 = 0.1246

lat2 = twoscore.6892

lon2 = 74.0445

impress (haversine(lat1, lon1,lat2, lon2), "1000.M." )

C#

using Organisation;

course GFG

{

static double haversine( double lat1, double lon1,

double lat2, double lon2)

{

double dLat = (Math.PI / 180) * (lat2 - lat1);

double dLon = (Math.PI / 180) * (lon2 - lon1);

lat1 = (Math.PI / 180) * (lat1);

lat2 = (Math.PI / 180) * (lat2);

double a = Math.Pow(Math.Sin(dLat / 2), ii) +

Math.Pow(Math.Sin(dLon / two), 2) *

Math.Cos(lat1) * Math.Cos(lat2);

double rad = 6371;

double c = 2 * Math.Asin(Math.Sqrt(a));

return rad * c;

}

public static void Primary()

{

double lat1 = 51.5007;

double lon1 = 0.1246;

double lat2 = 40.6892;

double lon2 = 74.0445;

Console.WriteLine(haversine(lat1, lon1,

lat2, lon2) + " K.Yard." );

}

}

PHP

<?php

function haversine( $lat1 , $lon1 ,

$lat2 , $lon2 )

{

$dLat = ( $lat2 - $lat1 ) *

M_PI / 180.0;

$dLon = ( $lon2 - $lon1 ) *

M_PI / 180.0;

$lat1 = ( $lat1 ) * M_PI / 180.0;

$lat2 = ( $lat2 ) * M_PI / 180.0;

$a = pow(sin( $dLat / 2), 2) +

prisoner of war(sin( $dLon / 2), ii) *

cos ( $lat1 ) * cos ( $lat2 );

$rad = 6371;

$c = 2 * asin(sqrt( $a ));

render $rad * $c ;

}

$lat1 = 51.5007;

$lon1 = 0.1246;

$lat2 = 40.6892;

$lon2 = 74.0445;

echo haversine( $lat1 , $lon1 ,

$lat2 , $lon2 ) .

" K.1000." ;

?>

Javascript

<script>

function haversine(lat1, lon1, lat2, lon2)

{

let dLat = (lat2 - lat1) * Math.PI / 180.0;

let dLon = (lon2 - lon1) * Math.PI / 180.0;

lat1 = (lat1) * Math.PI / 180.0;

lat2 = (lat2) * Math.PI / 180.0;

let a = Math.pow(Math.sin(dLat / 2), 2) +

Math.pow(Math.sin(dLon / 2), 2) *

Math.cos(lat1) *

Math.cos(lat2);

let rad = 6371;

let c = 2 * Math.asin(Math.sqrt(a));

return rad * c;

}

permit lat1 = 51.5007;

allow lon1 = 0.1246;

let lat2 = 40.6892;

let lon2 = 74.0445;

document.write(haversine(lat1, lon1, lat2, lon2) + " Yard.One thousand." );

</script>

Output:

5574.840456848555 K.Chiliad.

Source: https://www.geeksforgeeks.org/haversine-formula-to-find-distance-between-two-points-on-a-sphere/

Posted by: gentryfamenjusich.blogspot.com

Share this post